| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Heap
- 백준
- Articulation_Point
- singly Linked List
- data_structure
- template
- connected_component
- 예제
- Biconnected_Component
- c++
- Pair
- class_template
- 총정리
- deletion
- function_template
- '0'
- STL
- qsort
- red-black tree
- sstream
- list
- 구현
- 자료구조
- 13305
- Critical_Path_Analysis
- 문법
- sort
- Algorithm
- 5397
- 알고리즘
- Today
- Total
- Today
- Total
- 방명록
어제의 나보다 성장한 오늘의 나
[Algorithm] DFS 의 응용 사례(Topological sort , connected components , articulation point ... 등등) 본문
[Algorithm] DFS 의 응용 사례(Topological sort , connected components , articulation point ... 등등)
today_me 2022. 5. 15. 23:02오늘은 DFS의 응용 사례들에 대해서 알아보자
그 전에 DFS에 대해서 잘 모른다면 아래 포스터를 참고하면 DFS에 대해 배울 수 있다.
2022.05.15 - [Algorithm_Analysis] - [Algorithm] BFS 와 DFS
[Algorithm] BFS 와 DFS
BFS 와 DFS 용어 Discover : Vertex를 처음 방문했을 때 vertex를 discover 했다고 함 Explore : edge를 처음 방문했을 때 Finish : 자신의 노드 뿐만 아니라 연결된 노드들 모두 discovered 되었을 때 그 노드는..
8156217.tistory.com
DFS의 응용 사례
◎ Topological sort
◎ Finding connected component(undirected)
◎ Finding Strongly connected component(directed)
◎ Critical Path Analysis
◎ Biconnected Component (Articulation point) Problem
1. Topological sort
◎ DAG 여야 함 (Directed Acyclic Graph , directed 그래프이며 싸이클이 존재 하지 않는 그래프)
알고리듬
DFS를 하며 모든 vertex의 finish time을 구한다.
finish time의 내림차 순으로 vertex들을 정렬한다.
시간 복잡도

DFS를 실행 : 세타(V+E)
정렬 : constant - finish time이 정해질 때마다(finish time이 작은 것부터 정해지므로) 집어넣는다고 생각하면 constant 만큼 걸리므로 세타(V+E)이다.
이해하기 쉽게 옷 입는 순서를 예시로 topological sort를 풀어보자
아래 그림을 보면 옷을 입는 방식이 조금 정해져 있다.
descendant 인 vertex들은 반드시 parent를 실행 한 다음 실행에 옮겨져야 한다.
예를 들어 shirt -> tie -> jacket을 보면 이 순서로 입어야 한다. tie -> shirt 이런 순서는 불 가능하다.

시작은 어디서 부터 하든 지 상관없다. 여기서는 shirt에서 시작했다.
왼쪽 숫자는 start time , 오른쪽 숫자는 finish time이다.
finish time을 기준으로 내림차 순 정렬을 해보자

이렇게 하면 옷을 올바르게 입을 수 있다.
2. Connected Component( Undirected graph )
Connected Component들을 모두 구하는 문제이다.
◎ Undirected graph 대상
◎ BFS , DFS 모두 가능
알고리듬
아무 vertex에서나 DFS or BFS 를 실행 한다.
discover하는 vertex들의 id를 모두 통일 시킨다.
DFS or BFS가 끝나고 연결 되어 있지 않은 다른 component에서 DFS or BFS가 다시 진행 될 때는
다른 id로 통일 시킨다.
같은 component 끼리 같은 id를 지니고 있게 되어 구분이 된다.
간단하기 때문에 pass
3. Strongly Connected Component ( directed graph )
Strongly Connected Components 을 모두 구하는 문제이다.
이해 하기 쉽게 그림을 먼저 보자

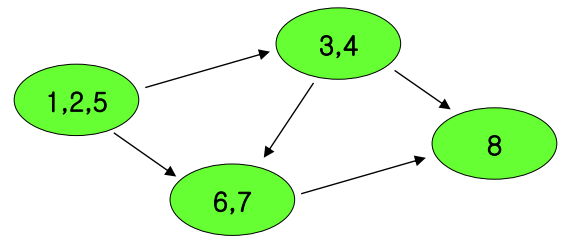
◎ 그래프의 Component 단위(오른쪽 그림)는 DAG( Directed Acyclic Graph ) 이다.
◎ Directed 그래프이다.
◎ Component 내에서 서로 왔다갔다 할 수 있어야 함.
알고리듬
1. DFS로 Finish time을 각각 구한다.
2. G를 전치 시킨다.
3. 1. 에서의 Finish Time이 컸던 순서대로 source vertex를 정해서 다시 DFS를 시작한다.
4. DFS를 마치면 component들을 모두 구했을 것이다.
Example
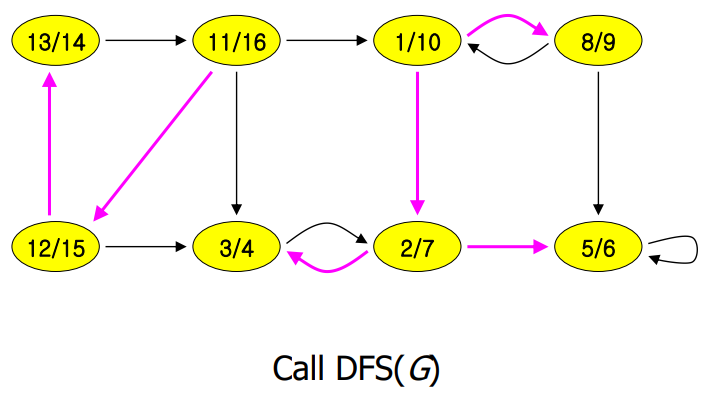
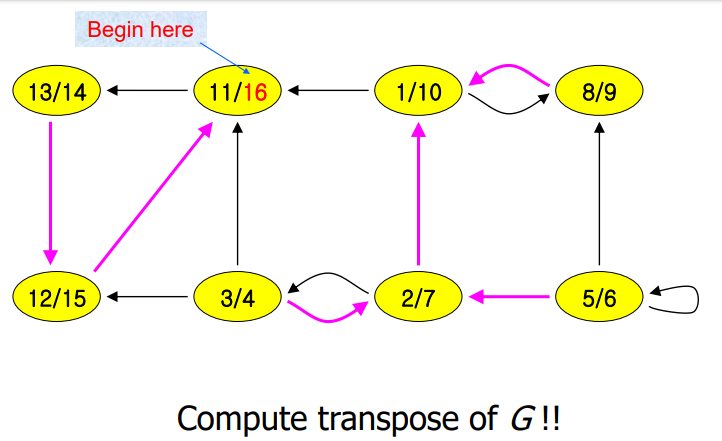

4. Critical Paths
start vertex 부터 end vertex 까지의 Path 중에서 weight가 가장 큰 Path를 찾는 문제이다.
◎ DAG 여야 한다.
◎ vertex들이 weight를 가지고 있다.
시간 복잡도

알고리듬
weight가 0 인 done 이라는 task를 넣어 준다. 이 것은 n+1 번째 task가 된다.
DAG의 edge들을 모두 reverse 해준다.
reverse 해주면서 vertex들의 weight를 edge가 가리키는 방향 바로 전 edge로 이동 시킨다.
예시를 보면 이해하기 쉽다.
Example

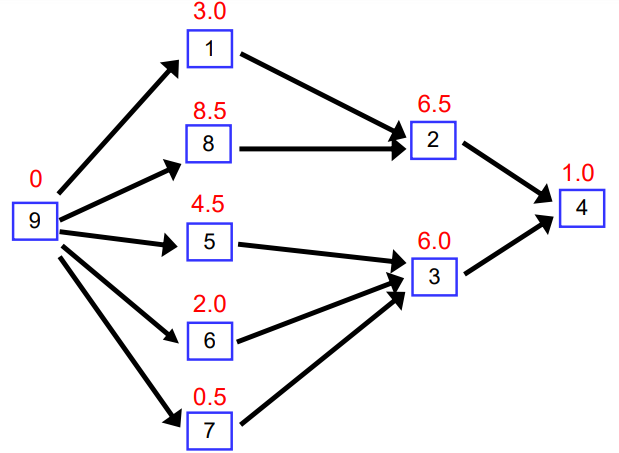
왼쪽 과 같은 문제가 있어서 Critical Path로 문제를 푸려고 한다.
오른쪽과 같은 DAG가 나올 때 이를 알고리듬 과정을 통해 풀어보자
각 노드는
est ( earlist start time )
eft ( earliest finish time )
를 가지고 있다.
est = 전 vertex들의 eft 중 가장 큰 값
eft = est + weight

오른쪽에 n+1 번째 task로 done을 삽입 하였다.
그리고 weight들을 edge로 옮겼다.
화살표도 모두 reverse 하였다.
맨 왼쪽 노드의 est 는 이제 시작 노드이므로 0으로 설정한다.
그럼 모든 준비가 끝난 것이다.

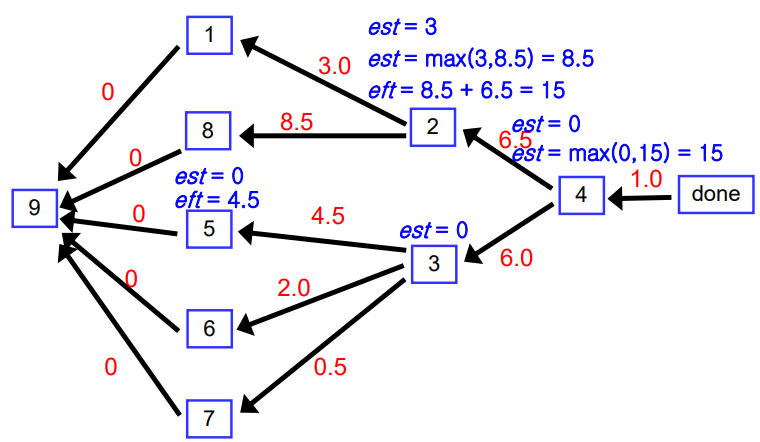



흐름을 다시 생각 해보면 이것은 DFS이다.
edge들을 reverse 시킨 뒤 DFS로 먼저 지나가는 vertex들의 esf들을 0으로 초기화 시킨다.
그리고 backtrack 하면서 est와 eft를 말했던 법칙에 따라 수정하는 것이다.
5. Bi-connected components ( Ariticulation Point )
두개의 components를 이어주는 Point를 Ariticulation Point라고 한다.
이 포인트인 vertex를 제거 하면 하나의 component가 두개의 components로 나누어 진다.
변수
d : discover time
back : articulation point 인지 확인 하는 변수
back 에 대해 좀 더 설명하자면 먼저 back은 d 값으로 초기화 한다.
그리고 back edge의(존재한다면) d 값 , child의 back값 , 현재 back 값을 비교한다.
그리고 작은 값을 back에 넣는다.
알고리듬
DFS로 내려가면서 d와 back을 초기화 해준다.
back은 이때 d로 초기화 된다.
그리고 더 내려갈 곳이 없으면 backtrack을 한다.
자신의 child의 back 값 >= 자신의 d값 이 성립 한다면 그 vertex는 articulation point이다.
이 것을 점검 한 뒤 위에서 설명 한 것 처럼 back을 비교 후 변경한다.
예시와 함께 보자
Example


y 노드의 경우 back은 5로 초기화 되었지만 back edge가 2 이므로 back은 2로 변경되었다.
x 노드의 경우 back은 4로 초기화 되었지만 back edge가 없지만 child의 back이 2 이므로 back이 2로 변경되었다.
v 노드의 경우 child의 back은 2 이고 자신의 d의 값이 2 이므로 v는 articulation point가 된다.
이렇게 다섯 가지 DFS 관련 문제를 살펴보았다
'Algorithm_Analysis' 카테고리의 다른 글
| [Algorithm][Sort] Counting sort( 계수 정렬 ) 총 정리 및 예제 (0) | 2022.05.27 |
|---|---|
| [Algorithm] Minimum Spanning Tree(MST) , Kruskal's algorithm , Prim's algorithm 총 정리 및 예제 (0) | 2022.05.18 |
| [Algorithm] [Graph - Shortest path] (1) Single source shortest path (0) | 2022.05.18 |
| [Algorithm] BFS 와 DFS (0) | 2022.05.15 |
| [Algorithm_analysis] Graph 용어 정리(Graph , tree , spanning..etc) (0) | 2022.05.15 |




