| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 백준
- connected_component
- 구현
- 문법
- Articulation_Point
- 예제
- 자료구조
- sstream
- function_template
- Algorithm
- qsort
- '0'
- STL
- 총정리
- Heap
- Pair
- 5397
- 13305
- class_template
- 알고리즘
- Critical_Path_Analysis
- deletion
- template
- Biconnected_Component
- singly Linked List
- list
- sort
- red-black tree
- data_structure
- c++
- Today
- Total
- Today
- Total
- 방명록
어제의 나보다 성장한 오늘의 나
[Algorithm_analysis] Graph 용어 정리(Graph , tree , spanning..etc) 본문
[Algorithm_analysis] Graph 용어 정리(Graph , tree , spanning..etc)
today_me 2022. 5. 15. 12:58Graph 란
◎ vertex와 edge로 구성된 한정된 자료구조를 의미
용어 정리
Value를 가지는 동그라미 부분 : Vertex or Node
vertex들을 이어 주는 부분 : Edge
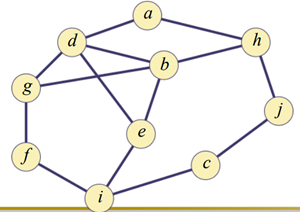
Degeree of a vertex : 특정 vertex와 연결 되어 있는 vertex의 개수
Directed graph : edge에 방향이 있는 그래프.
Undirected graph : edge에 방향이 없는 그래프
Weighted graph : edge에 weight가 주어진 그래프
Not Weighted graph : edge에 weight가 주어지지 않은 그래프

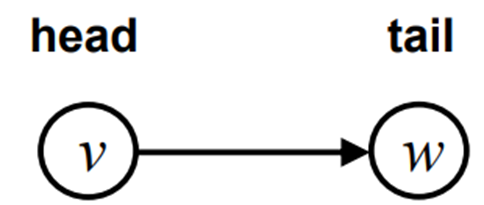
Directed 에서 시작하는 부분 : head
Directed 에서 타겟이 되는 부분 : tail
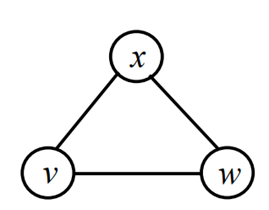
Symmetric digraph
Symmetric : 대칭적인
VW edge가 있으면 반대 되는 WV edge도 존재한다.

Complete graph
모든 vertices 사이에 edge가 존재
Complete graph의 edge의 개수
1. Undirected 의 경우 – n(n+1)/2 (n은 node 개수)
2. Directed 의 경우 – n(n-1)
Path and Cycle
Path는 연결된 vertices의 순서이다.
Simple path : 같은 vertice가 중복되지 않는 것

Cycle은 시작 노드와 끝나는 노드가 같을 수 있게 해 주는 것이다.
Simple Cycle : cycle path에 중복되는 노드가 없는 cycle.

Subgraph 와 spanning graph
Subgraph : 어떤 그래프에 포함 되는 그래프
Spanning graph : 어떤 그래프의 subgraph 중 모든 vertices들을 포함 하는 그래프
※ spanning graph는 특정 그래프의 vertices들은 모두 포함 해야 하지만 edge를 모두 포함할 필요는 없다.

Connected : 두 vertices 사이에 path가 있으면 connected 되었다고 한다.
Maximal connected subgraph : subgraph들 중 connected 되어 있으며 최대한 많은 vertices를 포함 하는 것.
Connected components : maximal connected subgraph 들로 이루어 진 집합
Strongly connected digraph : vertices 들 사이에 서로 reachable 하고 connected 되어 있는 것.
connected 와 strongly connected가 차이점이 없다고 생각 될 수 있다.
Strongly connected 는 digraph일 때 사용할 수 있는 것이다. 그래서 digraph가 아닐 때는 사용할 수 없다.

Acyclic : 싸이클이 없는
DAG : Directed Acyclic Graph의 준말
Tree : connected 그리고 acyclic 한 그래프
Spanning tree : 특정 그래프의 모든 vertices들을 포함 하는 데 tree인 것.

그래프를 나타내는 방법
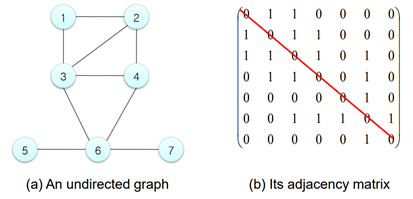
1) Adjacency Matrix
노드들 사이간의 관계를 0과 1을 이용하여 matrix로 나타내는 것
둘이 연결되어 있다면 1 아니라면 0
시간 복잡도 : O(V^2)
2) Adjacency List
각각의 Vertice 마다 연결된 vertices을 리스트로 만든 것
시간 복잡도 : O(V+E)





