| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 백준
- qsort
- STL
- data_structure
- 구현
- c++
- class_template
- function_template
- sort
- connected_component
- list
- 예제
- 13305
- Algorithm
- '0'
- 5397
- deletion
- Articulation_Point
- Biconnected_Component
- Heap
- Critical_Path_Analysis
- 문법
- sstream
- singly Linked List
- 알고리즘
- Pair
- 자료구조
- 총정리
- template
- red-black tree
- Today
- Total
- Today
- Total
- 방명록
어제의 나보다 성장한 오늘의 나
[Algorithm] Minimum Spanning Tree(MST) , Kruskal's algorithm , Prim's algorithm 총 정리 및 예제 본문
[Algorithm] Minimum Spanning Tree(MST) , Kruskal's algorithm , Prim's algorithm 총 정리 및 예제
today_me 2022. 5. 18. 22:14오늘은 Minimum spanning tree(MST)에 대해 알아보고 Graph에서 MST를 찾아내는 알고리즘 두 가지 (kruskal's algorithm , Prim's algorithm)에 대해서 알아 보자.
MST란?
Minimum : edge들의 weight의 총합이 가장 작다.
Spanning : 모든 vertex들을 포함 한다.
Tree : Cycle 이 없고 edge의 갯수가 vertex의 갯수-1 개 인 그래프.
이 세 가지 조건을 가진 것이 MST이다.
참고로 MST는 undirected graph에서만 정의 된다.
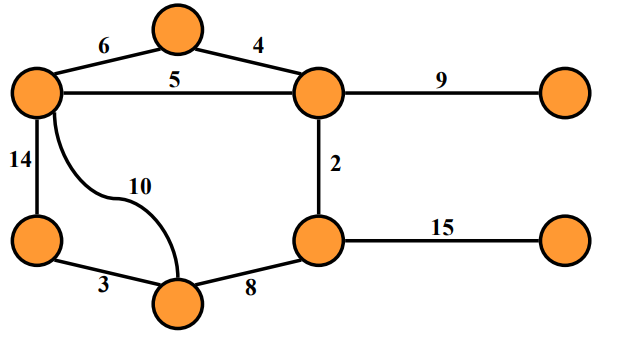
예를 들어 위와 같은 그래프가 있다고 했을 때 이 것의 MST는 아래와 같다.

확인해보자
edge들의 weight 총 합이 가장 작고,
모든 vertex들을 포함 하고,
Cycle이 없으며 edge의 갯수는 n-1 개인 graph이다.
MST가 맞다.
아래 그림에서 MST는 무엇일까?

a는 edge의 개수가 n-1개가 아니므로 X
d는 weight의 총합이 7 이므로 minimum이 아니므로 X
b와 c가 MST 이다.
그럼 특정 그래프에서 MST를 어떻게 구할 수 있을까?
그리디 알고리즘을 통해 구할 수 있다.
대표적인 그리디 알고리즘 두 가지를 알아보자
1. Kruskal's algorithm
알고리듬
edge들을 모두 내림차순으로 정렬한다.
edge들을 작은 값부터 하나씩 고른다.
만약 고른 edge가 list에서 cycle을 만들지 않는다면 list에 더한다.
이 것을 모든 edge에 대해서 반복한다.
Code

R은 모든 Edge를 담아 놓은 list
F 는 MST를 이루는 Edge들을 담아 놓는 list
Example


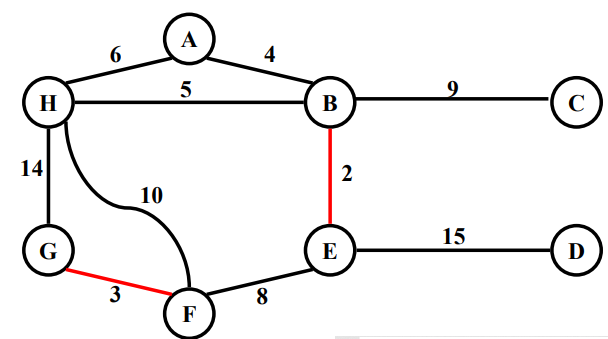
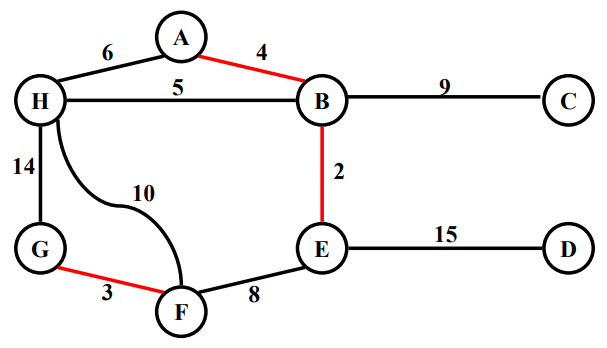

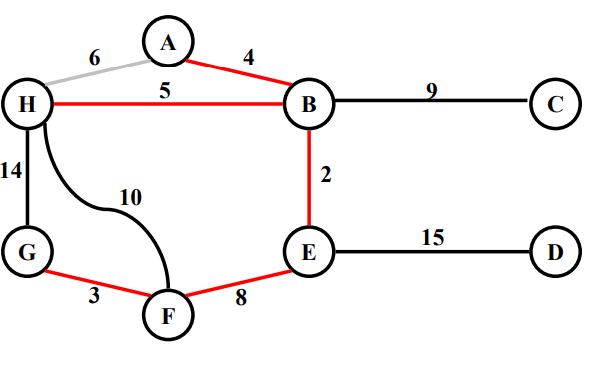


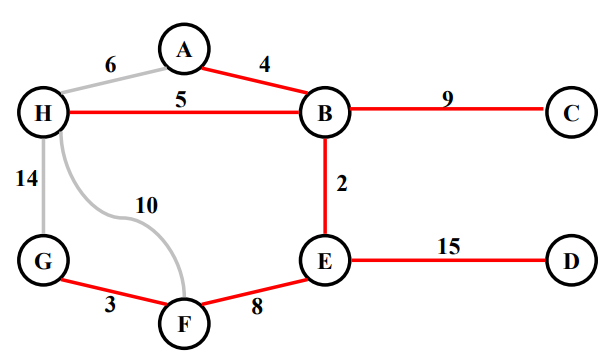
2. Prim's algorithm
알고리듬
임의의 vertex에서 시작한다.
시작하는 vertex의 값은 0으로 초기화 , 나머지는 무한대로 초기화
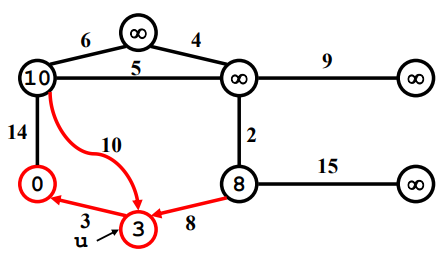
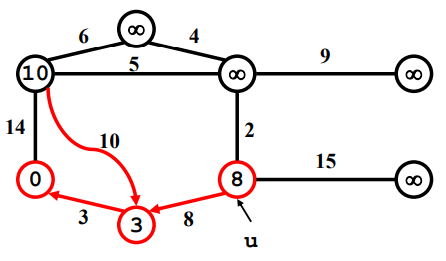
Priority queue를 사용하여 vertex 의 값이 제일 작은 vertex가 선택 된다. (처음에는 시작하는 vertex가 0 이므로 선택됨)
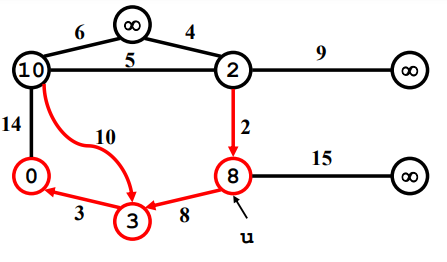
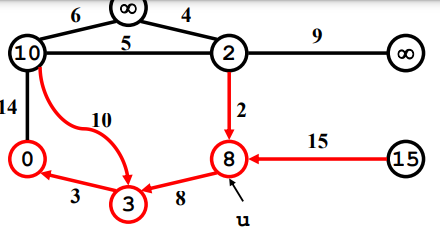
선택된 vertex와 연결된 vertex들의 값을 모두 체크한다.
만약 연결된 vertex들의 값이 연결된 edge weight 보다 크면 edge weight로 vertex의 값을 바꾼다.
선택 안됐던 vertex 중에서 vertex의 값이 가장 작은 vertex가 선택 된다.
... (위 의 과정 반복)
Code

ㅠ[v] 는 어디서 왔는지 조상을 나타내는 것이다.
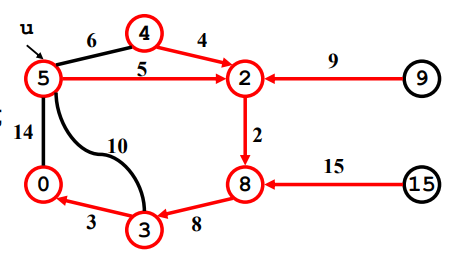
Example
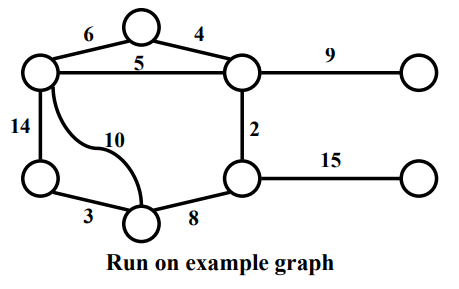

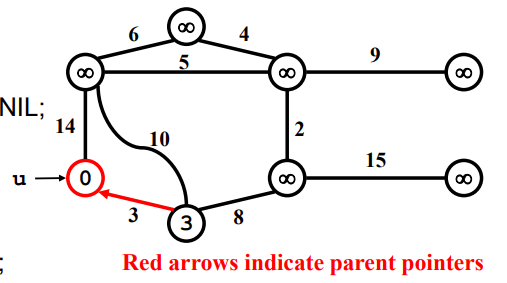

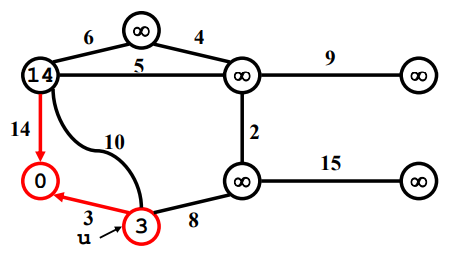








'Algorithm_Analysis' 카테고리의 다른 글
| [Algorithm] [Sort] Radix Sort ( 기수 정렬 ) (0) | 2022.05.27 |
|---|---|
| [Algorithm][Sort] Counting sort( 계수 정렬 ) 총 정리 및 예제 (0) | 2022.05.27 |
| [Algorithm] [Graph - Shortest path] (1) Single source shortest path (0) | 2022.05.18 |
| [Algorithm] DFS 의 응용 사례(Topological sort , connected components , articulation point ... 등등) (0) | 2022.05.15 |
| [Algorithm] BFS 와 DFS (0) | 2022.05.15 |




