| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 알고리즘
- singly Linked List
- STL
- 13305
- list
- 구현
- sort
- red-black tree
- data_structure
- 총정리
- qsort
- 문법
- Critical_Path_Analysis
- template
- 자료구조
- Pair
- c++
- sstream
- Algorithm
- '0'
- 예제
- Articulation_Point
- deletion
- class_template
- 백준
- 5397
- connected_component
- Heap
- Biconnected_Component
- function_template
- Today
- Total
- Today
- Total
- 방명록
어제의 나보다 성장한 오늘의 나
[Algorithm][Sort] Counting sort( 계수 정렬 ) 총 정리 및 예제 본문

오늘은 counting sort( 계수 정렬 )에 대해서 알아보려고 한다.
Counting sort는 다른 sort들에 비해 조건들이 추가적으로 더 있다.
그럼에도 불구하고 사용하는 이유는 조건들을 충족시키면 무려 θ(n)까지 가능 하다.
특징
◎ Stable sort
◎ Not Sort-In-Place
※ stable sort : 중복된 값을 가지는 원소들끼리의 순서가 sort 전/후로 바뀌지 않는 sorting
※ Sort-In-Place : 추가적인 메모리(추가 array) 없이 원소들이 담겨 있는 array에서 sorting 이 일어남
시간 복잡도
θ( n + k )
n : 원소의 개수
k : 원소 들의 값의 범위
( 만약 원소의 최대 값이 6 이라면 k는 6이고 원소들은 0~6 사이의 값을 가진다 )
Input / Output
◎ Input
array A[] : 0~k 사이의 값을 가진 원소가 n개 들어 있는 array.
◎ Output
array B[] : A 원소들이 sort 되어 있는 array.
◎ 추가 array
array C[] : A array의 원소들 중 C의 index보다 작거나 같은 원소들의 갯수를 저장.
array C는 k+1개의 원소를 가짐으로써 C의 index로 array A 원소 값 범위(0~k)를 나타냄
조건
◎ Input array의 원소들은 INTEGER 값을 가짐
◎ Input array의 원소들은 0~k 사이의 값을 가짐
◎ k는 O(n)
k가 만약 n^2이면 시간 복잡도는 θ( n + k ) -> θ( n^2 ) 이 되기 때문이다.
Base Algorithm
① array A의 원소를 x로 지정
② array A에서 x보다 작은 값이 몇 개 들어있는지 카운트
③ 만약 p개 있다고 했을 때 x는 p+1번째로 작은 값임
④ x를 array B 의 p+1 index에 집어 넣는다.
⑤ 모든 원소에 대해 진행
Sudo Code

4개의 for문으로 나누어 분석해 보자
Line 1~2 : initialization

array C 초기화
A 원소의 최대값 == 5
그러므로 K는 5 , C는 0~5 까지의 index를 가짐
Line 3~4 : Fill C array using A array

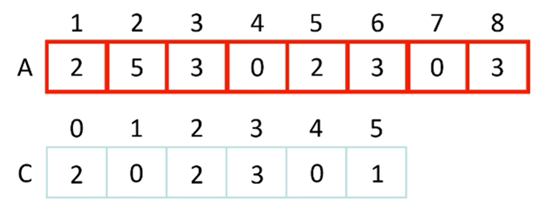
C는 A의 원소들의 갯수를 나타냄
c[0] ==2 는 A에 0이 두개 있다는 뜻
Line 5~6 : Complete C array


C는 A 원소들 중 C의 index 보다 작은 원소들의 갯수를 나타냄
Line 7~9 : Fill and Complete B array (Result)

j는 가장 끝부터 하나씩 감소한다.
즉 8부터 시작한다. 8 -> 1까지 온다.
A[8] == 3이다. 3은 C[3]==7을 통해 3 보다 작거나 같은 원소가 7개 있음을 알 수 있다.
3을 B[7]에 넣는다. 그리고 C[3]을 1 감소한다.
이 것을 j가 1일때까지 반복한다.

A[7] == 0 ; C[0] == 2 ; B[2] == 0; C[0]은 1 감소
따라서 C[0] == 1
계속 진행 하면 B는
B = {0 , 0 , 2 , 2 , 3 , 3 , 3 , 5}로 sort 된다.
+ 추가
시간 복잡도 계산
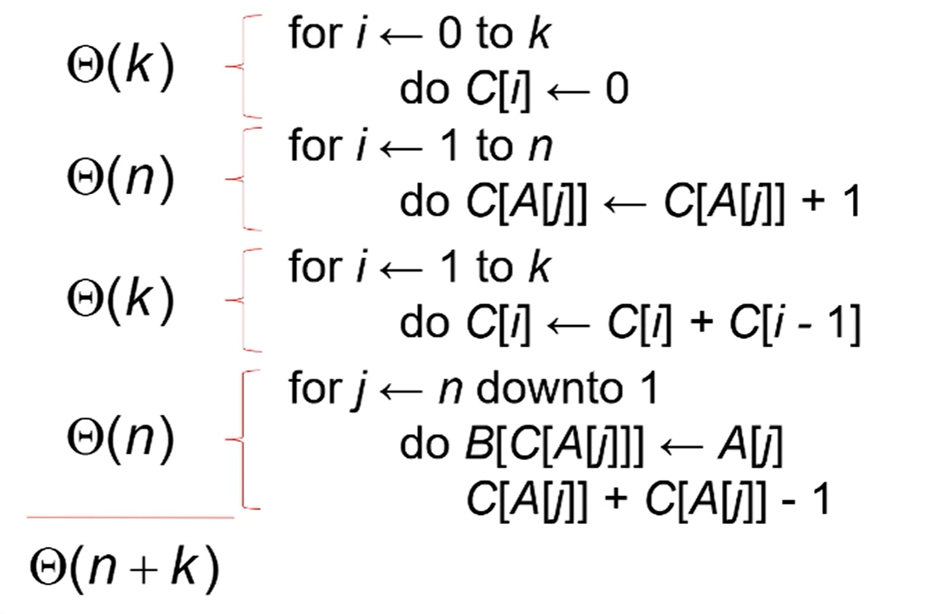
k = n^2 -> θ( n^2 )
k = n -> θ(n)




