| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- qsort
- red-black tree
- Biconnected_Component
- class_template
- Algorithm
- deletion
- sort
- sstream
- 총정리
- Articulation_Point
- 5397
- connected_component
- function_template
- Critical_Path_Analysis
- template
- list
- Pair
- 13305
- Heap
- 문법
- 백준
- STL
- singly Linked List
- data_structure
- c++
- 예제
- '0'
- 자료구조
- 알고리즘
- 구현
- Today
- Total
- Today
- Total
- 방명록
어제의 나보다 성장한 오늘의 나
[Algorithm] String Matching Problem (Naive Algorithm , Rabin-Karp Algorithm) 라빈 - 카프 알고리즘 본문
[Algorithm] String Matching Problem (Naive Algorithm , Rabin-Karp Algorithm) 라빈 - 카프 알고리즘
today_me 2022. 6. 6. 19:45String matching problem
특정 Text에서 주어진 Pattern이 나타나는 모든 index를 구한다.
이 때의 index를 valid shift 라고 부른다.
Valid shift Example

위 그림에서 Pattern P가 text T에서 index 3에서 나타난다. (s = 3 부분)
이 때 3은 valid shift 가 된다.
(Index 0 , 1 , 2는 각각 abca , bcab , caba로 pattern이 나타나지 않는다.
그래서 Index 0 , 1, 2는 invalid shift)
s = valid shift 일때
Text[s + i] = Pattern[i] 만족
valid shift를 모두 구하는 알고리즘 두 가지
1) Naïve - String - Matching Algorithm
2) Rabin - Karp - Algorithm
1) naïve – string – matching algorithm
Text의 index를 하나씩 증가시키며 Pattern과 일치하는 부분이 있는지 확인
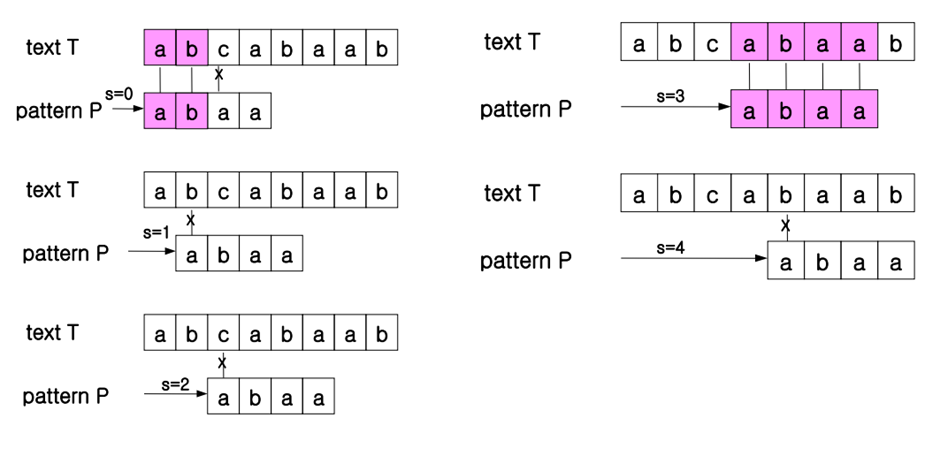
간단하다.
Sudo Code

시간 복잡도
Line 3 : Θ( n-m +1 )
Line 4 : O(m) -> s 한 번에 최소 1번 , 최대 m번 비교
전체 시간 복잡도 : O((n-m+1)m) -> m이 constant 면 O(n) , n/2이면 O(n^2)
좀 더 빠른 알고리즘을 알아보자
2) Rabin – Karp algorithm
문자열 매칭 문제를 숫자 비교 문제로 바꾸어서 해결하는 알고리즘
시간복잡도
Θ(n) -> 일반적인 케이스
과정
① Text 배열의 문자열을 d-진수의 숫자로 바꾸고
② pattern의 길이와 같은 substring들을 만든다.
③ substring들 중 pattern과 일치하는 것들이 몇개 있는지 확인
d-진수 ? substring? 이해가 안갈 테니 이해를 위해 example을 보자
Example
Pattern p = “31425” , Text T = “2359023141526739921” 이라고 하자.
아래는 문자열을 패턴과 같은 길이를 가진 substring들로 바꾼 결과이다.
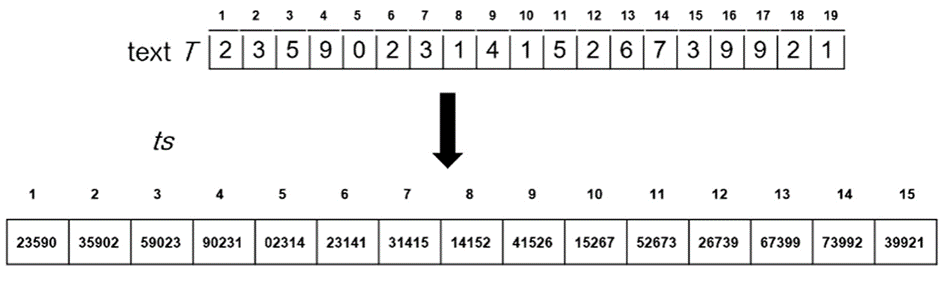
과정 설명
1) 문자열을 10-진수로 바꾼다. 왜냐하면 T에서 문자의 범위는 0~9 이므로 10개만 나오기 때문에 10-진수로 바꾸어준다. 만약 문자의 범위가 A~Z 까지 였다면 문자열을 26진수로 바꾸어주어야 한다.
2) 패턴 또한 바꾸어준다. 이 예시에서 Pattern p는 “31425” 에서 31,425로 바뀌었다.
3) 패턴의 길이 만큼 substring들을 만들어 새로운 배열에 집어넣는다. 패턴의 길이는 5이므로 text T의 index 0~4 , 1~5 , 2~6 … 이런식으로 잘라서 집어넣는다.
이 것이 알고리듬이다.
그럼 위 과정을 하면서 고민들이 생긴다.
문자열을 어떻게 숫자로 빠르게 변환 해줄 수 있을까?
그 과정에서 Horner’s rule을 사용한다.
◎ Horner’s rule
영국의 수학자 호너가 만든 다항식을 표현하는 법칙 중 하나
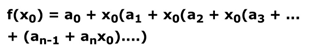
◎ 적용 : String P -> int p 로 바꾸기 ( 문자열 -> 숫자열)
P의 길이 m(pattern의 길이) 로 가정
Int p = P[m] + 10 *(P[m-1] + 10*(P[m-2] + 10 * (P[m-3] + … 10(P[2] + 10P[1]) ) ) )
Example
P = “31425” 라고 했을 때
왼쪽에서 오른쪽으로 스캔.
Step 1) 3
Step 2) 3*10 + 1
Step 3) (3*10 + 1)*10 + 4
Step 4) ((3*10 + 1)*10 + 4)*10 + 2
Step 5) (((3*10 + 1)*10 + 4)*10 + 2)*10 + 5
String P = “31425” -> Int p = 31,425
Horner’s rule 으로 변환 하는데 걸리는 시간 : Θ(m)
-> String이 m 자리라고 했을 때 곱하기를 m-1 번, 더하기를 m-1 번 해주기 때문이다.
Horner’s rule을 모든 substring에 적용해주면 substring이 int로 바뀐 값들을 얻을 수 있다.
근데 그렇게 되면 Θ(nm)만큼의 시간이 걸릴 것이다. (n은 substring 개수)
더 빠르게 변환 시켜 줄 수는 없을까??

Text T에서 맨 앞 다섯 자리 t_1 = 23590 을 Horner’s rule을 통해 구했다고 가정해보자.
그럼 그 다음 5자리를 변환 하기 위해서 또 Horner’s rule을 적용해야 할까?
앞의 숫자 5자리를 알고 있다면 그렇지 않고 더 빠르게 구하는 방법이 있다.
t_1 = 23590 , T[6] = 2 를 알고 있을 때
t_2 = 10 * ( t_1 – 10000 * T[1] ) + T[6]
= 10 * (23590 – 10000 * 2 ) + 2
= 35902
맨 앞의 숫자를 삭제하고 맨 뒤 숫자를 추가해 주는 방식이다.
곱하기 두 번 , 빼기 한 번 , 더하기 한 번 총 4번의 연산을 한다.
이 방식은 숫자의 자릿수 (m)이 늘어나더라도 연산의 횟수는 유지 된다.
따라서 시간 복잡도는 Θ(1) 이다.
그럼 다시 돌아가서
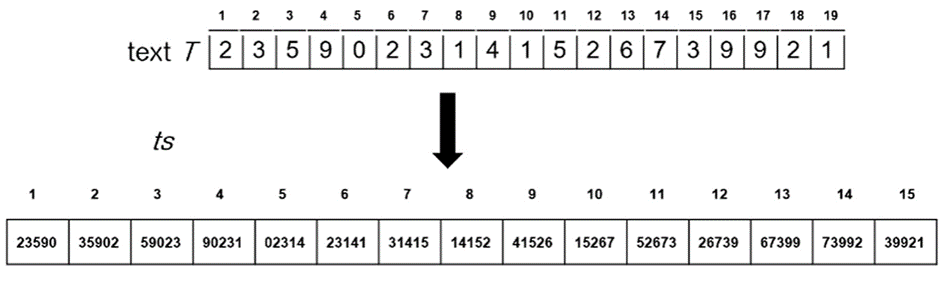
위의 과정은 시간이 얼마나 걸릴까?
M을 substring의 길이, n을 substring의 개수라고 했을 때
1 번의 horner’s rule (맨 처음) 과 n-m번의 앞의 것으로 다음 string 구하는 걸 사용해주면 된다.
전체 시간복잡도 : 세타 (m) + 세타(n-m) = 세타 (n)
빠르게 substring들의 int 버전을 모두 구했으니 이제 substring들과 패턴을 비교하여 같은 것들이 있는 지 알아봐야 한다.
Comparision
패턴과 substring 비교 하기
시간 복잡도 : Θ(1) -> 두개의 숫자를 비교하는 것이기 때문
일반 적인 케이스는 여기서 끝이다.
그래서 일반 적으로
Rabin – Karp algorithm의 시간복잡도는
Substring의 숫자열 구하기 + 비교 = Θ(n) + Θ(1) = Θ(n) 이라고 한다.
( 크게 안 중요한 부분 넘어가셔도 됩니다! )
그런데 만약 두 숫자의 크기가 엄청 크다면…? 단순 비교로는 불가하다. Modulo operation 을 사용해야 한다.
Modulo operation : 나머지를 구하는 operation. 기호 %를 사용한다.
만약 엄청 큰 숫자 a 와 b를 비교할 때 단순 비교가 불가하다면 각각 숫자 c로 나눈 뒤 나머지를 비교하는 것이다.
a % c 와 b % c 를 비교하는 것이다.
비교 후 세 가지의 경우의 수
i) ( Valid Case ) a % c 와 b % c 가 같고 a = b 이다.
ii) ( Spurious hit Case) a % c 와 b % c 가 같지만 a != b 이다.
iii) ( Invalid Case) a % c != b % c
특정 수로 나눈 나머지가 같다고 해서 두 수가 같은 것은 아니다. 그래서 위와 같은 세 가지의 경우로 나눠볼 수 있다.
하지만 Invalid Case 처럼 나머지가 다르면 두 수는 같은 수가 될 수 없다.
Algorithm
우리는 먼저 substring들로부터 나머지들을 구한다. 패턴의 나머지도 구한다.
그리고 나머지들을 먼저 비교하고 같은 것들을 추린다.
추려진 것들만 나머지가 아닌 substring을 한자리 씩 비교하여 (단순 비교 x) 패턴과 같은 지 확인한다.
※ 나머지를 구할 때 나눌 값으로 보통 소수를 지정한다. 소수가 아닌 값으로 나누게 되면 추려지는 양이 많아진다. 그래서 확 간추리기 위해 나누는 값으로 소수를 사용하자.
Example

Pattern의 p의 13으로 나누었을 때의 나머지를 구한다. -> 7

substring들의 13으로 나눈 나머지들도 구한다.
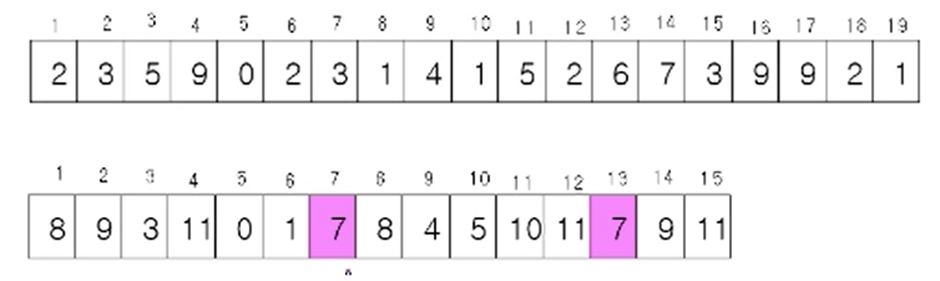
Pattern의 나머지 와 같은 것들 index 7 , index 13을 pattern과 비교한다.
Pattern p = 31415
T_7 = 31415 -> (Valid Case)
T_13 = 67399 -> (Spurious Hit Case)
더 빠르게 하는 방법
모든 substring의 나머지들을 구하지 않고 맨 처음 것만 구한다.

T_1 = 23590 , T_2 = 35902
T_2 = 10 * ( T_1 – T[1] * 10000 ) + T[6]
35902 = 10 * (23590 – 2 * 10000) + 2
T_2의 나머지는 오른쪽 항들을 모두 13으로 나눈 것을 계산 한 뒤
10 * ( 8 – 2 * 3 ) +2 = 22
결과를 13으로 나누고 나온 나머지가 된다.
22 % 13 = 9 (T_2 mod 13)
시간 복잡도 계산
Θ(1)
오른쪽 항을 천천히 살펴 보면 10000 과 10은 고정적인 값이므로 변하지 않는다.
그러므로 빼주는 맨 앞값(T[1]) 과 더해주는 맨 뒤값(T[6]) 만 매번 mod 해줘야 한다.
2번의 mod + 두번의 곱셈 + 한 번의 덧셈 + 한번의 뺄셈 = constant
전체 시간복잡도
Preprocessing
Pattern 숫자 변환 + mod 구하기 -> Θ(m)
Substring 맨 처음 꺼 숫자 변환 + mod 구하기 -> (m)
나머지 mod 구하기 -> Θ(n-m)
Find
worst case (모든 substring들의 mod가 pattern의 mod와 같을 때)
: Θ((n-m+1)m)
n-m+1 -> substring 개수
substring이 valid 한지 확인하는데 걸리는 시간 -> Θ(m)
따라서 worst case는 Θ(n+m) + Θ((n-m+1)m) = Θ((n-m+1)m)
Average case는 Θ(n+m) + Θ(m) = Θ(n+m)
정리
Rabin-karp algorithm은 naïve-string-algorithm을 좀 더 빠르게 해결하기 위해
문자열 비교 문제를 숫자열 비교 문제로 바꾸어 해결하는 algorithm이다.
그 과정에서 d-진수로 바꾸고
substring들을 구하고 숫자로 변환 시켜준다.
그리고 pattern과 compare한다.
그런데 compare할 때 두 숫자(패턴 과 substring)가 너무 크다면 단순 비교가 어렵기 때문에
먼저 substring들의 mod를 패턴의 mod와 비교하고 같은 것들을 추려서 비교를 한다.




