| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 총정리
- singly Linked List
- connected_component
- 알고리즘
- 5397
- sort
- template
- 구현
- data_structure
- sstream
- Articulation_Point
- STL
- class_template
- 백준
- qsort
- 자료구조
- 예제
- deletion
- list
- Heap
- Critical_Path_Analysis
- Pair
- 문법
- red-black tree
- 13305
- c++
- Algorithm
- function_template
- Biconnected_Component
- '0'
- Today
- Total
- Today
- Total
- 방명록
어제의 나보다 성장한 오늘의 나
[Algorithm] 순서 통계량 해결 알고리즘 (Medians and Order Statistics : <Randomized Selection> <Worst-Case Linear-Time Selection> ) 본문
[Algorithm] 순서 통계량 해결 알고리즘 (Medians and Order Statistics : <Randomized Selection> <Worst-Case Linear-Time Selection> )
today_me 2022. 6. 7. 03:18
i-th order statistic 란??
i 번째로 작은 원소를 뜻한다.
The Selection Problem 란??
i 번째 작은 원소를 찾는 것이다.
오늘은 세 가지 Selection Problem Algorithm에 대해서 배워 볼 것이다.
Selection Problem Algorithm 3 가지
1) Naive Algorithm
2) Randomized Selection
3) Worst-Case Linear-Time Selection
1) Naive Algorithm
정렬 후 i 번째 작은 값을 고르는 방법
시간 복잡도
Θ(n lgn)
merge sort + Pick i-th smallest element
= Θ(n lgn) + Θ(1)
= Θ(n lgn)
간단하지만 오래 걸린다.
2) Randomized Selection
랜덤하게 피벗 엘리먼트를 정하고 피벗을 기준으로 왼쪽에는 작은 값 , 오른쪽에는 큰 값이 있게 하고
이 것을 반복하여 i 번째 작은 값을 찾아내는 알고리즘
- Quicksort의 partition algorithm와 유사
시간 복잡도
Worst Case : Θ(n^2)
Average Case : Θ(n)
사진으로 보는 알고리듬

먼저 피벗 엘리 먼트를 정한다.
찾고자 하는 값이 피벗과 같다면 -> 그 값을 리턴한다.
찾고자 하는 값이 피벗 보다 크다면 -> 피벗 기준 오른쪽에 있는 서브배열( A[q+1 , r] )에서 다시 이 알고리즘을 적용한다.
찾고자 하는 값이 피벗 보다 작다면 -> 피벗 기준 왼쪽에 있는 서브배열( A[p , q-1])에서 다시 이 알고리즘을 적용한다.
Sudo code 와 함께 보자

<< 변수 설명 >>
p : 배열의 시작 index
r : 배열의 끝 index
q : 피벗의 index
k : 피벗의 배열에서의 상대적 위치
i : 배열에서 i 번째 작음을 나타내는 값 (찾는 값)
-----------------------------------------------------------------------------------------------------------------------------------------
<< Code 설명 >>
RandomizedPartition(A , p , r) -> 피벗의 index를 random하게 정해서 반환 ( q )
해주는 이유 : Worst case의 발생 확률을 낮추기 위함이다.
i가 k와 같다 -> 찾고자 하는 값이 피벗과 같다. A[q] 반환
i가 k보다 크다 -> 찾고자 하는 값이 피벗보다 크다. A[ p, q -1 ] 인 서브 배열에서 i를 찾음
i가 k보다 작다 -> 찾고자 하는 값이 피벗보다 작다. A[ q+1 , r ] 인 서브 배열에서 i-k 를 찾음
i-k인 이유는 i는 배열에서의 상대적 위치 이기 때문에 배열의 앞부분이 줄어들면 배열이 줄어든 만큼 i도 줄어들어야 하기 때문이다.
Average Case가 Θ(n)임을 증명
피벗으로 인해 1:9로 계속 해서 나뉜다고 가정
( Average 보다 안좋은 Case로 추론)
T(n) = T(9/10) + Θ(n) -> ( recursion tree ) -> Θ(n)
따라서 average Case의 경우 Θ(n)
Worst Case가 Θ(n^2)임을 증명
피벗 엘리먼트가 최소 or 최대만 골라진다고 가정
T(n) = T(n-1) + Θ(n)
-> Θ(n^2)
따라서 Worst Case 의 경우 Θ(n^2)
Worst Case도 Linear한 알고리즘은 없을까?
그 방법이 바로 세 번째 방법인 Worst-Case Linear-Time Selection 이다.
.
3) Worst-Case Linear-Time Selection
위에서 배운 RandomSelection함수를 이용하지만 Worst Case ( Θ(n^2) )가 나타날 수 없게
피벗을 중간 값으로 설정해주는 알고리듬
시간 복잡도
Worst Case : Θ(n)
알고리듬 순서
함수 이름은 Select(i , n) 이다
n개의 원소 중 i 번째 작은 값을 구하는 함수이다.

<Step 1>
5개를 원소를 갖는 그룹으로 나눈다.
시간 복잡도 : Θ(n)

<Step 2>
각 그룹의 중간 값을 구한다.
시간 복잡도 : Θ(n)
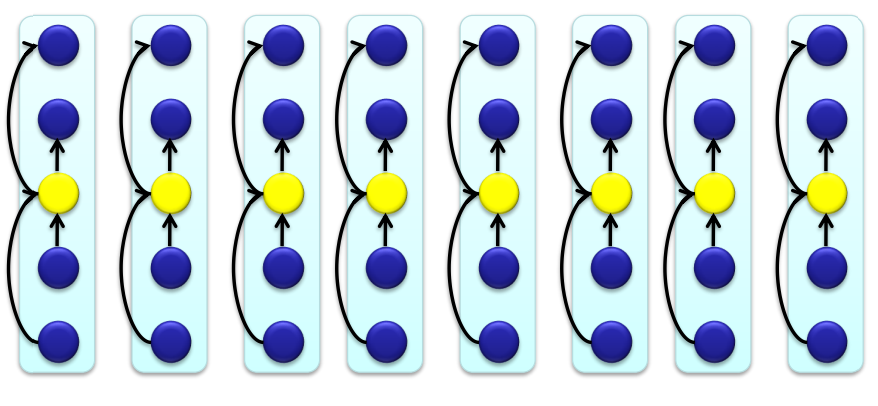
<Step 3>
select(i / 5 , n / 5 )함수를 recursive 하게 사용한다.
-> 중간 값들의 중간 값을 찾기 위함이다.
시간 복잡도 : T(n/5)

<Step 4>
pivot 주변 element들의 순서를 잘 조율한다.
pivot 보다 작은 값은 최소 3n/10 은 된다.
pivot 보다 큰 값은 최소 3n/10 은 된다.
나머지 4n/10 을 비교하여 pivot을 기준으로 잘 위치 시킨다.
시간 복잡도 : Θ(n)
Θ(4n/10) = Θ(n)
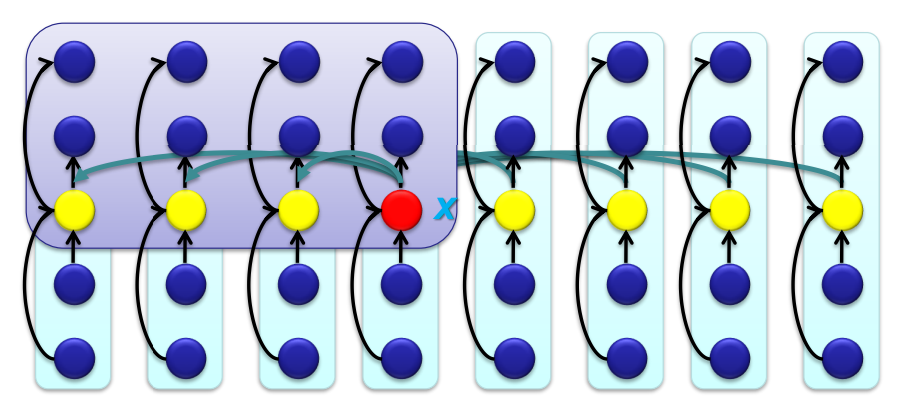
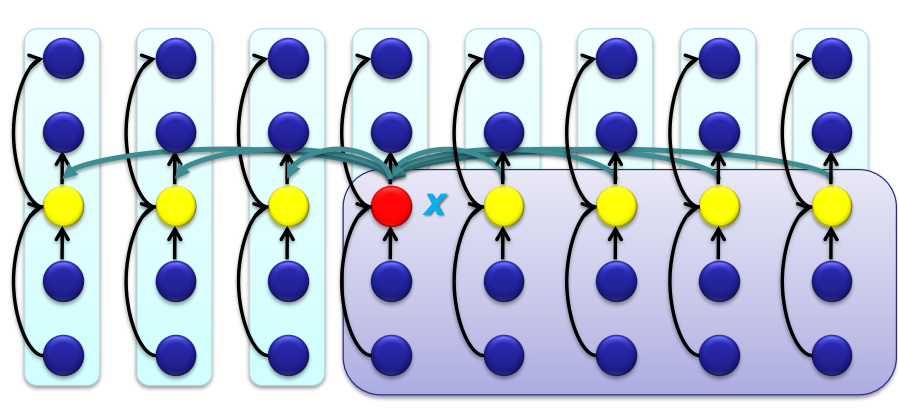
<Step 5>
피벗과 찾는 값 비교
피벗에 맞게 원소들을 위치 시켰으니 다음 과정인 피벗과 찾는 값을 비교하는 것을 진행한다.
값이 같으면 피벗 반환
값이 크거나 작으면 Select를 recursive하게 실행시킨다.
시간 복잡도 : T(7n/10)
Worst Case일 때 7n/10 : 3n/10 (7 : 3) 의 위치에 피벗이 있을 때이다.
7n/10 만큼을 가지고 Select함수를 recursive하게 돌려야 하기 때문이다.
전체 시간 복잡도
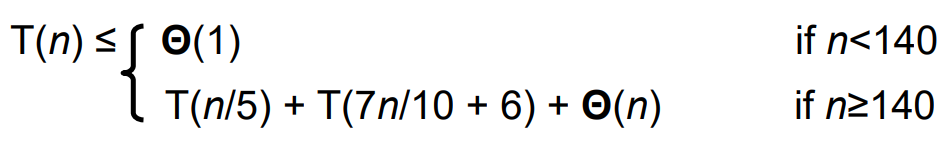
140이 어떻게 기준으로 정해지게 되었는 지는 모른다.
이 recurrence equation을 substitution으로 풀면
T(n) = Θ(n)
이렇게 세 가지의 Finding Order Statistics 알고리듬에 대해 알아 보았다.
'Algorithm_Analysis' 카테고리의 다른 글
| [Algorithm] Red-Black Tree ( 원리 및 insertion 설명 ) (0) | 2022.06.10 |
|---|---|
| [Algorithm] [String Matching Problem] Knuth-Morris-Pratt Algorithm 총 정리 및 예시 (0) | 2022.06.09 |
| [Algorithm] String Matching Problem (Naive Algorithm , Rabin-Karp Algorithm) 라빈 - 카프 알고리즘 (0) | 2022.06.06 |
| [Algorithm] [Sort] Radix Sort ( 기수 정렬 ) (0) | 2022.05.27 |
| [Algorithm][Sort] Counting sort( 계수 정렬 ) 총 정리 및 예제 (0) | 2022.05.27 |




